SILNIKI WIATROWE

WSTĘP I TROCHĘ TEORII

Poniższe wiadomości opracowałem m.in. na podstawie wiadomości zawartych w niżej wymienionej literaturze:
1. W. Jagodziński „Silniki wiatrowe”, PWT, Warszawa 1959.
2. „Poradnik inżyniera mechanika” tom II, WNT Warszawa 1969.
3. „Mechanik” tom IV część I, PWT Warszawa 1954.
4. Władysław Niestoj „Profile modeli latających”, Wydawnictwo Komunikacji i Łączności, Warszawa 1980.
5. Informator z 1999 roku firmy GTB-Solaris, Przytyk 6/31, 01-962 Warszawa.
6. Jerzy Mirecki „Fizyka dla klasy I i II technikum i liceum zawodowego”, Wydawnictwa Szkolne i Pedagogiczne, Warszawa 1990.
7. I. N. Bronsztejn, K. A. Siemiendiajew „Matematyka. Poradnik encyklopedyczny”, Wydawnictwo Naukowe PWN, Warszawa 1996.

            Sposób obliczeń wiatraka opiera się na założeniach upraszczających bardzo złożone zjawiska przepływu rzeczywistego powietrza, tzn. przyjmuje się, że wirnik znajduje się w ograniczonym obszarze ustalonego, osiowo symetrycznego, laminarnego przepływu powietrza uważanego za ośrodek nieściśliwy. Wszelkie zmiany energii i natężenia przepływu wzdłuż strug przebiegają zgodnie z równaniem ciągłości przepływu i prawem Bernoulliego, z wyjątkiem obszaru biegu wirnika (tzn. obszaru wyznaczonego przez łopatki obracającego się wirnika), gdzie ruch staje się nieustalony [3].

            Warunek ciągłości przepływu mówi o tym, że podczas przepływu strugi cieczy (w naszym przypadku powietrza) jej masa nie może ginąć, ani się zjawiać, czyli masy powietrza m₁ i m₂ przepływające przez przekroje A₁ i A₂ (rys.5) w jednostce czasu t są sobie równe.

m₁ = m₂

gdzie r - gęstość powietrza,

          v - średnia prędkość powietrza w strudze dla danego przekroju A.

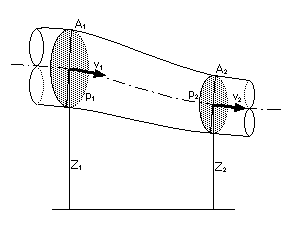
Rys.5

Ponieważ przyjmujemy uproszczenie, że powietrze jest nieściśliwe, więc gęstość r=r₁=r₂, czyli równanie ciągłości przyjmie postać:

Wynika z niego, że objętość powietrza przepływającego przez jakikolwiek przekrój poprzeczny strugi w jednostce czasu musi być równa objętości powietrza dopływającego do strugi, jak również z niej odpływającego. Z równania wynika też, że prędkość przepływu v jest odwrotnie proporcjonalna do powierzchni poprzecznego przekroju strugi A [1].

            Prawo Bernoulliego wyraża zasadę zachowania energii przystosowaną do przepływu strugi cieczy (powietrza). Masa powietrza m przepływającego przez przekrój A (rys.5) posiada pewien zasób energii, na który składa się [1]:

-         energia ruchu (kinetyczna)

-         energia ciśnienia p (równoważna pracy nacisku p×A na drodze v×t )

-         energia potencjalna wzniesienia masy m na wysokość Z względem obranego poziomu gdzie g - przyśpieszenie ziemskie w [m/s²].

Podczas przepływu bez strat energie dla przekrojów A₁ i A₂ (rys.5) muszą być sobie równe, zatem

ponieważ ciężar właściwy  [N/m³], a gęstość  (V-objętość w [m³]), więc , czyli masa . Podstawiamy do równania energii wzór na m:

Objętość, gęstość i ciężar właściwy powietrza są takie same w każdym przekroju strugi (V=V₁=V₂, r=r ₁=r ₂, g=g ₁=g ₂). Za r×g podstawiamy g i dzielimy równanie przez g×V. Otrzymujemy równanie Bernoulliego:

Poszczególne człony tego równania wyrażają:

   - wysokość prędkości (z tej wysokości musiałoby spaść ciało, aby w swobodnym spadku mogło uzyskać prędkość v),

       - wysokość ciśnienia (wysokość słupa powietrza, wywierającego swoim ciężarem ciśnienie p),

   Z       -   wysokość położenia.

Zgodnie więc z równaniem Bernoulliego suma wysokości prędkości, wysokości ciśnienia i wysokości położenia jest stałą wzdłuż danej strugi [1].

Koło wiatrowe może dać moc tylko przez pobranie przez nie mocy od przepływającego powietrza. Może to nastąpić kosztem zmniejszenia prędkości wiatru (z v₀ do v₂, rys.6), czyli przez częściowe jego zahamowanie przez koło wiatrowe. Wobec zmiany prędkości wiatru przed i za kołem wiatrowym i wobec zachowania ciągłości przepływu, przekrój strumienia powietrza dopływającego do koła wiatrowego (A₀) musi być odpowiednio mniejszy (prędkość v₀ większa), zaś przekrój strumienia powietrza za kołem wiatrowym (A₂) musi być odpowiednio większy (prędkość v₂ mniejsza). Na to zjawisko ma jeszcze wpływ zmiana ciśnienia powietrza w sąsiedztwie koła wiatrowego. Już na pewnej odległości przed kołem wiatrowym na skutek stopniowego zahamowywania wiatru występuje spiętrzenie ciśnienia powietrza (do p₁), natomiast tuż za kołem wiatrowym występuje zmniejszenie ciśnienia powietrza (do p₂), które dopiero na pewnej odległości wyrównuje się z ciśnieniem otoczenia (p₀) [1]

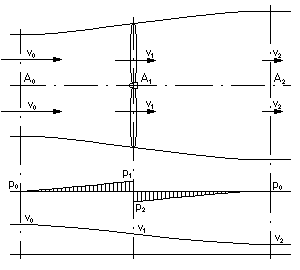
Rys.6 

W rzeczywistym wiatraku na skutek spiętrzenia ciśnienia część powietrza odpływa na zewnątrz koła, ale ta strata na razie nie będzie uwzględniana. Zmiana prędkości wiatru odbywa się także na pewnej odległości przed i za kołem wiatrowym, ale przyjmiemy, że następuje raptownie w samym kole wiatrowym [1].

Prędkość v₁, z jaką powietrze przepływa przez koło wiatrowe nie jest znana. Ponieważ jednak prędkość ta musi być jakąś pośrednią pomiędzy v₀ i v₂, przyjmiemy, że jest ich średnią arytmetyczną [1]:

Masa m przepływającego powietrza w każdym z przekrojów jest stała i wynosi:

          [kg]

gdzie:

            r - gęstość powietrza [kg/m³],

             t - czas [s],

            D - średnica zewnętrzna koła wiatrowego [m].

Gęstość powietrza r można obliczyć dla dowolnego ciśnienia p [Pa] i temperatury powietrza temp [°C] wg wzoru:

gdzie p₀ [Pa] i temp₀ [K] to ciśnienie i temperatura dla znanej gęstości r₀ [kg/m³] [1]. Ponieważ dla gęstości powietrza 1,2928 [kg/m³] temperatura powietrza i ciśnienie wynoszą odpowiednio 273,15 [K] i 101325 [Pa] to wzór na gęstość dla dowolnej temperatury [°C] i ciśnienia powietrza [Pa] będzie wyglądał następująco:

Strumień powietrza dopływający do koła wiatrowego z prędkością v₀ posiada energię kinetyczną [1]:

a odpływający:

Gdy koło wiatrowe pobiera energię bez żadnych strat, to energia ta:

Dzieląc energię wykorzystaną przez wiatrak DE przez energię wiatru E_K0 otrzymamy teoretyczny współczynnik wykorzystania wiatru x_t:

Ze wzoru na DE wynika, że im większa różnica pomiędzy prędkościami v₀ i v₂, tym większa będzie energia przejmowana przez wiatrak, czyli lepszy współczynnik x_t. Jednak prędkość v₂ musi być większa od 0, ponieważ aby wiatrak działał powietrze musi przez niego przepływać. Przyjmuje się, że stosunek v₂/v₀ powinien być równy jak 1 do 3 [1]. Oznacza to, że dla uzyskania największego współczynnika wykorzystania energii wiatru prędkość odlotowa powietrza za kołem wiatrowym (v₂) musi wynosić 1/3 dolotowej prędkości wiatru. Prędkość wiatru w samym kole wiatrowym (v₁):

Zatem wszystkie trzy przyjęte charakterystyczne prędkości (v₀, v₁, v₂) wiatru przy największym jego wykorzystaniu są względem siebie w następującym stosunku:

v₀ : v₁ : v₂ = 3 : 2 : 1

wtedy x_t osiąga maksymalną wartość równą 0,593 [1].

            Moment obrotowy silnika wiatrowego powstaje w wyniku działania wiatru na łopaty wirnika (rys.7 i 8) [2]. 

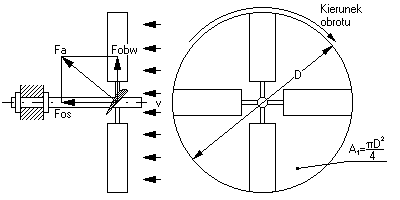
Rys.7 

Siła aerodynamiczna Fa jest wypadkową siły oporu Fx powstałej wskutek naporu powietrza na łopatkę i siły nośnej Fy, której mechanizm powstawania jest nieco bardziej skomplikowany. Otóż przyjmuje się, że ilość powietrza napływającego na krawędź natarcia łopatki o profilu np. płasko-wypukłym jest równa ilości powietrza spływającego z krawędzi spływu (zgodnie z równaniem ciągłości strugi). Ponieważ górna powierzchnia łopatki ma większą krzywiznę niż dolna, górna struga ma do przebycia w tej samej jednostce czasu dłuższą drogę, czyli jej prędkość jest większa niż dolnej. Zgodnie z prawem Bernoulliego ciśnienie górnej strugi będzie mniejsze niż dolnej. Ta różnica ciśnień jest główną przyczyną powstawania siły nośnej. Także na łopatce o przekroju symetrycznym może powstawać siła nośna, jeśli łopatka jest ustawiona pod dodatnim kątem natarcia (kąt a na rys.8). W takim przypadku opływ strugi powietrza na górnej i dolnej powierzchni będzie niesymetryczny, prędkość powietrza na górnej powierzchni będzie większa niż na dolnej, powstanie więc różnica ciśnień, a w wyniku tego siła nośna [4].

Siła aerodynamiczna Fa może być rozłożona na składową styczną do płaszczyzny obrotów wirnika Fobw i normalną Fos. Składowa styczna powoduje obrót, a składowa normalna wywołuje nacisk osiowy, który jest przejmowany przez łożyska. Rozkład siły aerodynamicznej przedstawia rys.8. Cięciwa profilu łopaty w pewnym przekroju odległym o r od osi wirnika tworzy z płaszczyzną wirnika kąt zaklinowania j. Prędkość wiatru v ma kierunek prostopadły do płaszczyzny wirnika. Uwzględniając prędkość obwodową (unoszenia) łopatki

gdzie n – prędkość obrotowa w [obr/min]

wynikającą z ruchu obrotowego koła wiatrowego otrzymuje się prędkość względną w strugi powietrza

W stosunku do cięciwy profilu prędkość ta tworzy z cięciwą profilu kąt natarcia a, a z płaszczyzną obrotu kąt napływu prędkości względnej b [2].

 
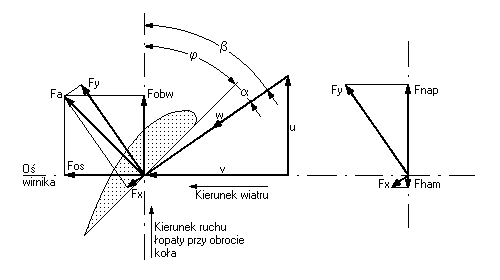
Rys.8 

Siły nośną Fy i oporu Fx wyznacza się w oparciu o charakterystykę profilu z wzorów [2]:

gdzie Cy - współczynnik aerodynamiczny siły nośnej Fy,

         Cx - współczynnik aerodynamiczny siły oporu Fx,

współczynniki Cy i Cx dobiera się z charakterystyki profilu w zależności od kąta natarcia a (rys.11),

         r - gęstość powietrza w [kg/m³],

         A – powierzchnia wycinka łopaty o wymiarach s× l (rys.9 i 10) w [m²].

Na rysunku nr 8 można zauważyć, że pomiędzy cięciwą profilu i siłą aerodynamiczną Fa oraz pomiędzy prędkością względną w i siłą nośną Fy są kąty proste. A stąd wynika, że pomiędzy siłą Fa i osią wirnika jest kąt b-a, pomiędzy Fy i Fa kąt a. Można więc wyprowadzić wzór na siłę wywierającą nacisk osiowy Fos:

Jeśli z rzutujemy siły Fx i Fy na płaszczyznę obrotu to otrzymamy z Fx siłę przeciwdziałającą obrotowi wirnika Fham (siłę hamującą), a z Fy siłę działającą zgodnie z kierunkiem obrotu wirnika Fnap (napędzającą). Między siłami Fx i Fham oraz między Fy i osią obrotu jest kąt b (rys.8). Z tych i poprzednich zależności (sinb=v/w, cosb=u/w) wyprowadzić można wzory na Fham i Fnap:

Różnica Fnap i Fham to nic innego jak siła obwodowa Fobw, czyli siła powodująca obrót koła wiatrowego:

         Łopatkę wirnika dzieli się na pewną ilość elementów (rys.9 i 10), dla których przeprowadza się obliczenia prędkości, kątów i sił, ponieważ wraz ze wzrostem promienia r rośnie też wartość prędkości obwodowej u, co powoduje zmianę prędkości w i kąta b. Dla każdego elementu (jego przekroju) dobiera się kąt zaklinowania j tak, aby uzyskać właściwy kąt natarcia a (co jest warunkiem uzyskania prawidłowej pracy łopatki). Kąt a dobiera się najczęściej jako równy lub bliski kątowi maksymalnej doskonałości profilu (jest to kąt, dla którego stosunek Cy/Cx osiąga maksymalną wartość). Łopatka wiatraka jest więc zwichrowana, a kąt zaklinowania j zmienia się od wartości największej u nasady (od środka) do najmniejszej przy końcówce łopaty (średnica zewnętrzna koła wiatrowego) [2].

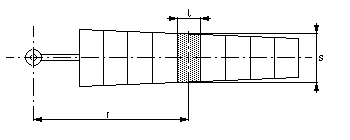
Rys.9

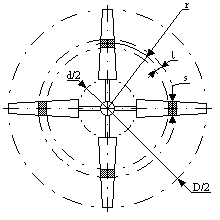
Rys.10

Jak wcześniej wspomniano siły Fy i Fx oblicza się wykorzystując współczynniki Cy i Cx (spotyka się także oznaczenia współczynnika Cy jako Cz). Wartości tych współczynników wyznacza się doświadczalnie podczas odmuchiwania płatów o różnych profilach w tunelach aerodynamicznych, dokonując pomiaru sił Fy i Fx dla różnych kątów natarcia, a następnie oblicza się Cy i Cx z przekształconych wzorów na Fy i Fx [1]:

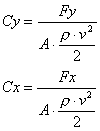
gdzie v – prędkość powietrza napływającego na płat.

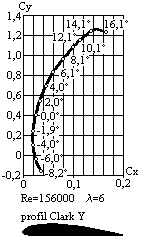
Rys.11

Uzyskane wyniki podaje się w postaci wykresów Cy(a), Cx(a) lub najczęściej jako wykres funkcji Cy(Cx) (nazywany biegunową profilu) z zaznaczonymi kątami natarcia profilu (rys.11). Wielkości Cy i Cx zależą nie tylko od kształtu profilu, jego kąta natarcia, szybkości wiatru, ale i od stosunku długości płata l do szerokości s (w tym przypadku mowa o wymiarach całego płata, skrzydła, a nie wycinku łopatki). Dzieje się tak, ponieważ na skutek różnicy ciśnień nad i pod płatem następuje przepływ powietrza na końcach spod jego spodu na jego wierzch (rys.12). Ten ruch powietrza nakłada się na ruch powietrza napływającego na płat, a będąc do niego prostopadłym, wywołuje dwa wiry rozciągające się za końcami płata. Energia potrzebna do wytworzenia tych wirów może być dostarczona tylko przez płat, co ujawnia się dla niego jako pokonywanie pewnego oporu nazywanego oporem indukcyjnym (wzbudzonym). Opór ten jest tym mniejszy im stosunek długości do szerokości jest większy [4].

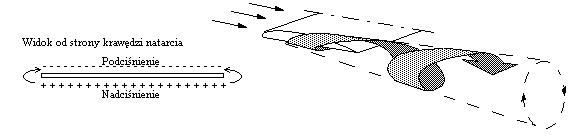
Rys.12

Wpływa on również na zmniejszenie kąta natarcia przy końcach płata. Stosunek l do s nazywa się rozpiętością względną albo wydłużeniem l:

Charakterystykę profilu sporządza się najczęściej dla l = 5 lub l = ¥ (dane dla l = ¥ uzyskuje się np. przez zastosowanie rozpiętości płata większej lub równej szerokości tunelu aerodynamicznego).

Ponieważ powietrze nie opływa łopatki równomiernie, tzn. prędkość powietrza względem łopatki (w) rośnie wraz z odległością od środka do średnicy zewnętrznej koła wiatrowego, przyjmuje się najczęściej profile o l = ¥. Jeśli charakterystyka profilu jest wyznaczona dla innej wartości l, np. równej 5, to można przeliczyć współczynniki Cy i Cx oraz kąt natarcia a dla l = ¥ wykorzystując poniższe wzory [3]:

Dla wyznaczonej biegunowej profilu podaje się też tzw. liczbę Reynoldsa [4]:

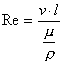
gdzie:

v – prędkość powietrza, m/s,

l – długość profilu, m,

m - współczynnik tarcia wewnętrznego, kg/m×s,

r - gęstość powietrza, kg/m³.

Stosunek m do r nazywany jest kinematycznym współczynnikiem lepkości n, który w warunkach tzw. atmosfery normalnej (temperatura 15 [°C], ciśnienie 101357 [Pa], gęstość 1.225 [kg/m³]) przyjmuje wartość 0.0000143 [m²/s]. Czyli Re równa się [4]:

Re = 70000× v× l

Gdy dwa płaty o profilach geometrycznie podobnych (posiadających wymiary liniowe proporcjonalne, a kąty jednakowe) znajdują się w strumieniach powietrza o pewnych prędkościach, to przepływy tego powietrza wokół płatów są mechanicznie podobne pod warunkiem, że liczba Reynoldsa jest dla nich taka sama (iloczyn prędkości powietrza i długości cięciwy każdego z profili muszą być sobie równe). Z warunku tego wynika, że prędkość w tunelu aerodynamicznym powinna być tyle razy większa od prędkości wiatru, ile razy jest mniejszy badany profil od tego zastosowanego w łopatce [1]. Liczba Re jest różna dla łopatki w zależności od promienia łopatki i jej szerokości. Dla uproszczenia w wiatrakach o małych mocach (o średnicach do 10 [m]) można przyjąć jeden profil o ustalonej liczbie Re. Do tego celu można zastosować profile stosowane w modelarstwie lotniczym (o Re bliskich 200000, 400000).

Szerokość łopatki s oblicza się na podstawie zasady równości zmiany pędu i popędu poruszającego się ciała (powietrza).

Pędem ciała nazywamy iloczyn jego masy i prędkości (m× v) [6].

Popędem lub impulsem siły nazywamy iloczyn jej wartości i czasu przez jaki działa (F× t) [6].

 Zmiana pędu ciała jest równa popędowi siły działającej na to ciało [6]:

F× t = D(m× v)

F× t = ( m× v₁) - (m× v₂) = m× (v₁- v₂)

W naszym przypadku powietrze o masie m zmienia swoją prędkość z v₀ do v₂ (zmiana pędu = m×(v₀-v₂) ). Dzieje się to pod wpływem działania na nie siły hamującej, pochodzącej od koła wiatrowego, równej co do wartości sile osiowej Fos, lecz o przeciwnym zwrocie (popęd siły = Fos× t). Ponieważ przeprowadzamy obliczenia łopaty dzieląc ją na mniejsze elementy (rys.9) o wymiarach l× s, to masę m będzie stanowić powietrze przepływające przez pierścień o powierzchni p×(r+l/2)²-p×(r-l/2)²=2×p×r×l (rys.10). Natomiast siłę Fos liczy się dla jednego wycinka (l× s) łopaty pomnożonego przez liczbę łopat i. Można więc przekształcić równanie zmiany pędu i popędu siły jak poniżej:

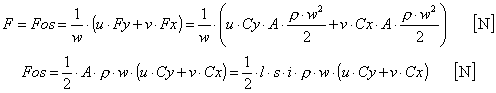
czyli F× t = m× (v₁- v₂) przyjmie postać:

Stąd mamy szerokość łopatki s:

Moc jednego wycinka łopatki jest równa iloczynowi siły Fobw i prędkości obwodowej u dla tego elementu, a moc wiatraka jest sumą mocy poszczególnych elementów jednej łopatki pomnożonej przez ilość łopatek i i przez sprawność wiatraka.

gdzie:

n – liczba elementów obliczeniowych na które podzielono łopatkę (rys.9),

k – numer kolejnego elementu,

Fobw_k – siła obwodowa dla k-tego elementu,

u_k – prędkość obwodowa dla k-tego elementu,

h_a – sprawność aerodynamiczna silnika wiatrowego,

h_m – sprawność mechaniczna silnika wiatrowego.

Moment obrotowy jest sumą momentów poszczególnych elementów jednej łopatki pomnożonej przez ilość łopatek oraz przez sprawność wiatraka.

gdzie:

n – liczba elementów obliczeniowych na które podzielono łopatkę,

k – numer kolejnego elementu,

Fobw_k – siła obwodowa dla k-tego elementu,

r_k – promień (odległość od osi wirnika do środka k-tego wycinka),

h_a – sprawność aerodynamiczna silnika wiatrowego,

h_m – sprawność mechaniczna silnika wiatrowego.

Sprawność mechaniczna h_m wiatraka uwzględnia straty powstałe w wyniku tarcia w łożyskach i przekładniach. Natomiast sprawność aerodynamiczna h_a to straty wywołane oporem indukowanym profilu, odpływem powietrza na zewnątrz koła wiatrowego, zawirowaniem powietrza za wiatrakiem (ruch śrubowy powietrza przeciwny do obrotów wiatraka), oporem profilowym (zależy od gładkości powierzchni łopat) oraz oporem interferencyjnym (spowodowany jest wzajemnym oddziaływaniem sąsiednich łopatek na przepływ powietrza, zwłaszcza w częściach przylegających do piasty).

Do wstępnego określenia mocy wiatraka o średnicy D można obliczyć moc wiatru przepływającego przez płaszczyznę omiataną łopatkami i pomnożyć ją przez współczynnik wykorzystania (x_t) energii wiatru i sprawność wiatraka (h_a, h_m). Moc wtedy będzie równa:

Dla szybkobieżnego silnika wiatrowego można np. przyjąć x_t=0.593, h_a=0.64, h_m=0.8. Można też przekształcić ten wzór do następującej postaci:

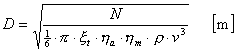
Możemy za jego pomocą obliczyć jaką powinien mieć średnicę silnik wiatrowy, aby uzyskał moc użyteczną N.

            W celu porównania właściwości wiatraków podawane są takie parametry jak rzeczywisty współczynnik wykorzystania wiatru (x = x_t × h_a × h_m ), współczynnik momentu obrotowego y (równy momentowi wiatraka podzielonemu przez energię strugi wiatru) oraz wyróżnik szybkobieżności Z (jest to stosunek prędkości obwodowej końca łopatki do prędkości wiatru). Na poniższym rysunku przedstawiono charakterystyki x i y w funkcji Z dla kilku typów silników wiatrowych.

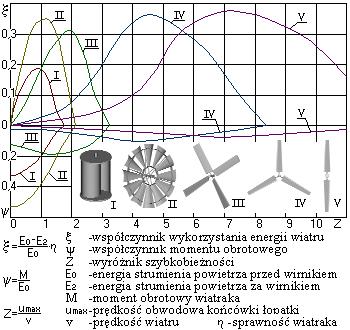
Rys.13

Wiatrak należy zaopatrzyć w możliwość nastawiania pod wiatr oraz w urządzenia regulujące obroty, moc itp. 

Ochronę antypiorunową można wykonać na dwa sposoby:

1. Każde skrzydło zaopatrujemy w odpowiedni przewód piorunochronowy przyłączony do metalowego pierścienia osadzonego na wale i wraz z nim się obracającego. Do pierścienia dotyka metalowa płytka (szczotka) połączona z drugą płytką ślizgającą się po metalowym pierścieniu umieszczonym na słupie, maszcie czy wieży wiatraka i odpowiednio uziemionego.

2. Sposób mniej pewny – piorunochron umieszczamy na odpowiednio wysokim słupie umieszczonym obok wiatraka. Wiatrak powinien znajdować się w przestrzeni stożka o wysokości i promieniu podstawy równym wysokości słupa.

 www.darmowa-energia.eko.org.pl